喊你来讲题!
把知识讲给别人是最高效的学习方法!学习金字塔理论和费曼学习法都证明了这一点。咔咔来讲为你提供一个平台,请你来解答下列问题,并将解题过程录制出来,让你因‘分享知识’而进步,让知识因‘被分享’而更有意义。
题目1
如图,在$\triangle ABC$中,$\angle BAC=\displaystyle\frac{2\pi}{3}$,点$D$在线段$BC$上,$AD\perp AC$,$\displaystyle\frac{BD}{CD}=\frac{1}{4}$,求$\sin C.$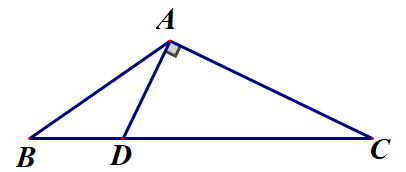
答案
答案:$\displaystyle\frac{\sqrt{21}}{10}$.题目2
在锐角$\triangle ABC$中,角$A$,$B$,$C$所对的边为$a$,$b$,$c$,若$\displaystyle\frac{\sin B\sin C}{3\sin A} = \frac{\cos A}{a} + \frac{\cos C}{c}$且$\sin^2 A + \sin^2 B – \sin^2 C = \sin A \cdot \sin B$,求$\displaystyle\frac{c^2}{a + b}$的取值范围。答案
答案:$[\sqrt{3},2)$.题目3
$△ABC$的内角$A、B、C$的对边分别为$a,b,c,$已知$(c – 2b)\cos A + \displaystyle \frac{a^2 + b^2 – c^2}{2b} = 0$(1)若$a = 4$,$b + c = 8$,求$△ABC$的面积;
(2)若角$C$为钝角,求$\displaystyle \frac{c}{b}$的取值范围.
答案
答案:$(1) S=4\sqrt{3}; (2) (2,+\infty)$.题目4
记\(\triangle ABC\)的内角\(A,B,C\)的对边分别为\(a,b,c\),已知\(\triangle ABC\)的面积为\(\sqrt{3}\),\(D\)为\(BC\)中点,且\(AD = 1\).(1)若\(\angle ADC = \displaystyle \frac{\pi}{3}\),求\(\tan B\);
(2)若\(b^2 + c^2 = 8\),求\(b,c\).
答案
答案:$(1) \tan B=\displaystyle\frac{\sqrt{3}}{5}; (2) b=c=2$.题目5
在$\triangle ABC$中,内角$A$,$B$,$C$的对边分别为$a$,$b$,$c$,点$O$是$\triangle ABC$的外心,$a\cos(C – \displaystyle \frac{\pi}{3}) = \displaystyle \frac{\overrightarrow{AO} \cdot \overrightarrow{AB}}{|\overrightarrow{AB}|} + \frac{\overrightarrow{AO} \cdot \overrightarrow{AC}}{|\overrightarrow{AC}|}$。(1)求角$A$;
(2)若$\triangle ABC$外接圆的周长为$4\sqrt{3}\pi$,求$\triangle ABC$周长的取值范围。
答案
答案:$(1) A=\frac{\pi}{3}; (2) (12,18]$.题目6
在 \(\triangle ABC\) 中,内角 \(A, B, C\) 的对边分别为 \(a, b, c\),且 \(c = 2b\),\(2\sin A = 3\sin 2C\)。(1) 求 \(\displaystyle \frac{a}{b}\) 的值;
(2) 若 \(\triangle ABC\) 的面积为 \(\displaystyle \frac{3\sqrt{7}}{2}\),求 \(AB\) 边上的高。
答案
答案:$(1) \frac{a}{b}=\frac{3\sqrt{2}}{2}; (2) \frac{3\sqrt{7}}{4}$.题目7
(多选题) 在斜三角形 \( ABC \) 中,\( A \)、\( B \)、\( C \) 对应边分别为 \( a \)、\( b \)、\( c \),\( \sin A = \cos B \),则( )
A. \( \triangle ABC \) 为锐角三角形
B. 若 \( a=1 \),则 \( b=\tan B \)
C. \( 2\tan B + \tan C \) 最小值为 \( \displaystyle\frac{5\sqrt{3}}{3} \)
D. \( 1 < \cos A + \cos B + \cos C \leq \displaystyle\frac{5}{4} \)
答案
答案:$BCD$.题目8
记\(\triangle ABC\)的内角\(A,B,C\)的对边分别为\(a,b,c\),已知\(a\cos B – c = \sqrt{3}a\sin B\),\(a = 3\).(1)求\(A\);
(2)若点\(D\)是边\(BC\)上靠近\(C\)的三等分点,且\(AB \perp AD\),求\(AD\)的长.
答案
答案:$(1) A=\displaystyle \frac{5\pi}{6}; (2) AD=\displaystyle\frac{\sqrt{7}}{7}$.题目9
已知$\triangle ABC$为锐角三角形,$\sin(A-B)=\dfrac{\sqrt{2}}{10}$,且$\tan C=7$.(1) 求$\sin A\cos B$;
(2) 求$B$;
(3) 若$\triangle ABC$的面积为$7$,求$\triangle ABC$外接圆的周长.
