本题由2023级25班孙宁梓讲解!
[ratemypost]
题目展示——先探究、再听讲
题目1 如图,在$\triangle ABC$中,$\angle BAC=\displaystyle\frac{2\pi}{3}$,点$D$在线段$BC$上,$AD\perp AC$,$\displaystyle\frac{BD}{CD}=\frac{1}{4}$,求$\sin C.$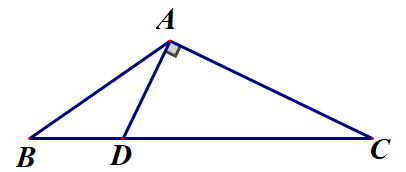
解题探究——点击直达
答案解析
在△ABD中, $ \displaystyle\frac{BD}{\sin\displaystyle\frac{\pi}{6}} =\displaystyle \frac{AD}{\sin B}$$ \therefore \displaystyle\frac{n}{\sin\displaystyle\frac{\pi}{6}} = \displaystyle\frac{4n\sin C}{\sin B}$
$ \therefore\displaystyle\frac{1}{\displaystyle\frac{1}{2}} =\displaystyle \frac{4\sin C}{\sin( \displaystyle\frac{2\pi}{3}-C)}$
$\therefore2 = \displaystyle\frac{4\sin C}{\displaystyle\frac{\sqrt{3}}{2}\cos C -\displaystyle \frac{1}{2}\sin C}$
$\therefore\begin{cases} 5\sin C = \sqrt{3}\cos C \\ \sin^2 C + \cos^2 C = 1 \end{cases}$
$\therefore\sin C =\displaystyle \frac{\sqrt{21}}{14}$
