观看人数: 159
三角函数的图象和性质
1.解下列方程和不等式.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
(1)\sin x=0;(2)\sin x=1;(3)\cos x \ge \frac{1}{2} ;(4)\tan x \ge 1;(5)\sin x\ge \cos x.~~~~~~~~~~~~~~~~~~~~~~~~~~ 答案
答案:(1)x=k\pi,k\in Z;(2)x=\frac{\pi}{2}+2k\pi,k\in Z;(3)[-\frac{\pi}{3}+2k\pi,\frac{\pi}{3}+2k\pi],k\in Z;~~~~~~~~~\\(4)[\frac{\pi}{4}+k\pi,\frac{\pi}{2}+k\pi),k\in Z;(5)[\frac{\pi}{4}+2k\pi,\frac{5\pi}{4}+2k\pi],k\in Z.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 2.已知函数f(x)=\sin(2x-\frac{\pi }{3}),求f(x)的周期、对称轴、对称中心、单增区间.~~~~~~~~~~~~~ 答案
答案:周期T=\pi;对称轴x=\frac{5\pi}{12}+\frac{k\pi}{2},k\in Z;对称中心(\frac{\pi}{6}+\frac{k\pi}{2},0),k\in Z;~~~~~~~~~~~~~~~~~~\\单增区间[-\frac{\pi}{12}+k\pi,\frac{5\pi}{12}+k\pi],k\in Z.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 变式.已知函数f(x)=\sin(-2x+\frac{\pi }{3}),求单增区间.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 答案
答案:[\frac{5\pi}{12}+k\pi,\frac{11\pi}{12}+k\pi],k\in Z;提示:转化为f(x)=-\sin(2x-\frac{\pi }{3}).~~~~~~~~~~~~~~~~~~~~~~~~~ 3.下列区间中, 函数 f(x)=7 \sin \left(x-\frac{\pi}{6}\right) 单调递增的区间是( ~~)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ \begin{array}{lll}A.\left(0, \displaystyle\frac{\pi}{2}\right) &B.\left(\displaystyle\frac{\pi}{2}, \pi\right) \quad C.\left(\pi, \displaystyle\frac{3 \pi}{2}\right) &D.\left(\displaystyle\frac{3 \pi}{2}, 2 \pi\right)\end{array} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案: A;提示:注意“单调递增的区间”与“单调递增区间”的区别,代入选项验证即可。\\
当 0 < x < \frac{\pi}{2} 时, -\frac{\pi}{6} < x-\frac{\pi}{6} < \frac{\pi}{3} , 所以 f(x) 在 \left(0, \frac{\pi}{2}\right) 上单调递增, 故 A 正确.~~~~~~~~~~~~~~~~
4.设函数 f(x)=\cos \left(\frac{\pi}{3}-2 x\right) , 则 f(x) 在 \left[0, \frac{\pi}{2}\right] 上的单调递减区间是 (\quad) ~~~~~~~~~~~~~~~~~~~~~~~\\
A. \left[0, \frac{\pi}{6}\right] ~~
B. \left[0, \frac{\pi}{3}\right] ~~
C. \left[\frac{\pi}{3}, \frac{\pi}{2}\right] ~~
D. \left[\frac{\pi}{6}, \frac{\pi}{2}\right] ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案: D;
提示:变形为 f(x)=\cos \left(2 x-\frac{\pi}{3}\right), 2 k \pi \leqslant 2 x-\frac{\pi}{3} \leqslant 2 k \pi+\pi, k \in \mathbf{Z}, ~~~~~~~~~~~~~\\k \pi+\frac{\pi}{6} \leqslant x \leqslant k \pi+\frac{2 \pi}{3} ,
k \in \mathbf{Z} , 又 x \in\left[0, \frac{\pi}{2}\right], \therefore 单调递减区间为 \left[\frac{\pi}{6}, \frac{\pi}{2}\right] .~~~~~~~~~~~~~~~~~~~~~~~
5. 已知 \omega>0 , 函数 f(x)=\frac{1}{2} \cos \omega x-\frac{\sqrt{3}}{2} \sin (\pi-\omega x) 在 \left(\frac{\pi}{3}, \frac{\pi}{2}\right) 上单调递增, 则 \omega 的~~~~~~~\\取值范围是(~~)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
A. [2,6] ~~
B. (2,6) ~~
C. \left[2, \frac{10}{3}\right] ~~
D. \left(2, \frac{10}{3}\right) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 答案
答案 :C;提示:化简得 f(x)=\cos \left(\omega x+\frac{\pi}{3}\right) , 单增区间为[\frac{1}{\omega}(2k\pi-\frac{4\pi}{3}),\frac{1}{\omega}(2k\pi-\frac{\pi}{3})],\\又 f(x) 在 \left(\frac{\pi}{3}, \frac{\pi}{2}\right) 上单调递增,\therefore \left(\frac{\pi}{3}, \frac{\pi}{2}\right)为单增区间的子集,\therefore
\left\{\begin{array}{l}\frac{1}{\omega}(2k\pi-\frac{4\pi}{3}) \le \frac{\pi}{3}, \\\frac{1}{\omega}(2k\pi-\frac{\pi}{3}) \ge \ \frac{\pi}{2},\end{array}\right. \\ 解得 6 k-4 \le \omega \le 4 k-\frac{2}{3} , 所以 2 \le \omega \le \frac{10}{3} .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 变式1.已知函数 f(x)=\sin \left(\omega x+\frac{\pi}{6}\right)(\omega>0) 在区间 \left[-\frac{\pi}{4}, \frac{2 \pi}{3}\right] 上单调递增, 求 \omega 的取~~~\\值范围.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案: 0<\omega \leqslant \frac{1}{2};
方法同上, \left\{\begin{array}{l}\omega \leqslant \displaystyle\frac{8}{3}-8 k, k \in \mathbf{Z}, \\ \omega \leqslant \displaystyle\frac{1}{2}+3 k, k \in \mathbf{Z},\end{array}\right. 所以 k=0时 0<\omega \leqslant \frac{1}{2} .
~~~~~~~~~~~~~~~~~ 变式2.已知函数 f(x)=\sin \omega x(\omega>0) 在区间 \left[-\frac{\pi}{4}, \frac{ \pi}{3}\right] 上单调递增, 求 \omega 的取值范围.~~~~~~ 答案
答案:(0,\frac{3}{2}];提示: f(x)=\sin \omega x图象过原点,\frac{T}{4}\ge\frac{ \pi}{3},\Rightarrow \omega \le\frac{3}{2}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 6.已知函数f(x)=\sin(2x-\frac{\pi }{3}+\varphi )为偶函数,求\varphi 的最小正值.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 答案
答案:\frac{5\pi }{6} ;提示:-\frac{\pi }{3} +\varphi =\frac{\pi }{2} +k\pi ,\varphi 的最小正值为\frac{5\pi }{6} .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 变式1.已知函数f(x)=\sin(2x-\frac{\pi }{3}+\varphi )为奇函数,求\varphi 的最小正值.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 答案
答案:答案:\frac{\pi }{3} ;提示:-\frac{\pi }{3} +\varphi =k\pi ,\varphi 的最小正值为\frac{\pi }{3} .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 变式2. 将函数 y=2 \sin \left(2 x+\frac{\pi}{3}\right) 的图像左移 m(m>0) 个单位后图象关于y轴对称,~~~~~~~\\求 m 的最小值.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 答案
答案:\frac{\pi }{12} ;提示:平移m后y=2\sin (2x+2m+\frac{\pi }{3} ),\because 函数为偶函数,\therefore 2m+\frac{\pi }{3} ~~~~~~~~~~\\=\frac{\pi }{2}
+ k\pi ,\therefore m最小为\frac{\pi }{12} .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 7.(1)求函数y=\sin x+\cos x 的值域.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ (2)求函数 y=\sin x-\cos \left(x+\frac{\pi}{6}\right),x\in[0,\pi] 的值域. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ (3)求函数 y=\sin ^{2} x+\sqrt{3} \cos x-\frac{3}{4},x \in\left[0, \frac{\pi}{2}\right] 的值域.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(4)求函数 y=\sin x-\cos x+\sin x \cos x 的值域.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 答案
(1)答案: [-\sqrt{2}, \sqrt{2}] ;提示:y=\sqrt{2} \sin \left(x+\frac{\pi}{4}\right) ,\therefore值域为 [-\sqrt{2}, \sqrt{2}] .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ (2)答案: \left[-\frac{1}{2}, 1\right]
;提示: y=\sin x-\cos \left(x+\frac{\pi}{6}\right)=\frac{3}{2} \sin x-\frac{\sqrt{3}}{2} \cos x~~~~~~~~~~~~~~~~~~~~~~~~~\\=\sqrt{3} \sin \left(x-\frac{\pi}{6}\right) ,
x \in[0, \pi], x-\frac{\pi}{6} \in\left[-\frac{\pi}{6}, \frac{5 \pi}{6}\right] , 值域为 \left[-\frac{\sqrt3}{2}, \sqrt3\right].~~~~~~~~~~~~~~~~~~~~~~~~~~
(3) 答案:[\frac{1}{4},1];提示:y=-\cos ^{2} x+\sqrt{3} \cos x+\frac{1}{4} , 令 \cos x=t,则t \in[0,1],~~~~~~~~~~~~~~~~~~~\\y=-t^2+\sqrt{3}t+\frac{1}{4},
\therefore 值域为[\frac{1}{4},1]
.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ (4)答案: \left[-\frac{1}{2}-\sqrt{2}, 1\right] ;提示:设 t=\sin x-\cos x , 则 t^{2}=1-2 \sin x \cos x, \sin x \cos x~~~\\=\frac{1-t^{2}}{2} , 且 -\sqrt{2} \leqslant t \leqslant \sqrt{2} .
\therefore y=-\frac{t^{2}}{2}+t+\frac{1}{2},
\therefore 函数的值域为 \left[-\frac{1}{2}-\sqrt{2}, 1\right] .~~~~~~
函数y=Asin(ωx+φ)的图象及应用
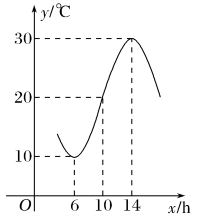
1. 某地一天 6 \sim 14 时的温度变化曲线近似满足函数 y=A \sin (\omega x+\varphi)+b(|\varphi|<\pi) , 求~~\\这段曲线的函数解析式.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案:y=10 \sin \left(\frac{\pi}{8} x+\varphi\right)+20 ;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\提示:周期 T=16, A=10, b=20 . \therefore \omega=\frac{\pi}{8}, ~~~~~~~~~~~~~~\\ \therefore y=10 \sin \left(\frac{\pi}{8} x+\varphi\right)+20,又图象经过 (6,10),~~~~~~~~~ \\\therefore \sin \left(\frac{3}{4} \pi+\varphi\right)=-1,|\varphi|<\pi, \therefore \varphi=\frac{3}{4} \pi . \therefore 函数的~\\解析式为 y= 10 \sin \left(\frac{\pi}{8} x+\frac{3 \pi}{4}\right)+20, x \in[6,14] .~~~~~~~
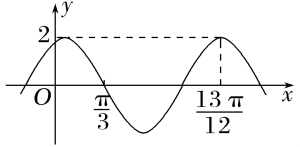
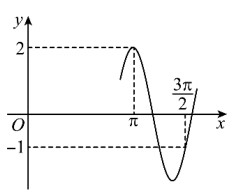
2.已知函数 f(x)=2 \cos (\omega x+\varphi)\left(\omega>0,|\varphi|<\frac{\pi}{2}\right) 的部分图象如图所示, 求 f\left(\frac{\pi}{2}\right).~~~~~~
答案
答案:-\sqrt{3} ;提示:由题图可知 \frac{3}{4} T=\frac{3 \pi}{4} , ~~~~~~~~~\\即 T=\pi, \omega=2 , 故 f(x)=2 \cos (2 x+\varphi) . ~~~~~~~~~~\\点\left ( \frac{13 \pi}{12}, 2 \right ) 在图象上,\Rightarrow \varphi=-\frac{\pi}{6} .~~~~~~~~~~~~~~~\\所以 f\left(\frac{\pi}{2}\right)=-\sqrt{3} .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
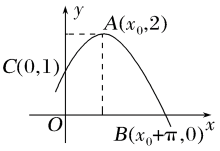
3.已知函数 f(x)=A \sin (\omega x+4 \varphi)\left(A>0, \omega>0,0<\varphi<\frac{\pi}{8}\right) 的部分图象如图所示, ~~~~\\求函数解析式.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案:f(x)=2 \sin \left(\frac{1}{2} x+\frac{\pi}{6}\right);~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\提示: A=2, T=4 \pi=\frac{2 \pi}{\omega} , 解得 \omega=\frac{1}{2} , ~~~~~~~~~~~~~~~~~~~\\故 f(x)=2 \sin \left(\frac{1}{2} x+4 \varphi\right) .
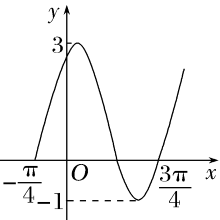
因为图象过点 C(0,1) , \\\therefore \sin 4 \varphi=\frac{1}{2} , 且点 (0,1) 在单增区间上,4 \varphi=\frac{\pi}{6}+2 k \pi, \\0<\varphi<\frac{\pi}{8}, 4 \varphi=\frac{\pi}{6}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 4.函数 f(x)=A \sin (\omega x+\varphi)+b\left(A>0, \omega>0,|\varphi|<\frac{\pi}{2}\right) 的部分图象如图所示,求 f\left(\frac{\pi}{2}\right).
答案
答案:1-\sqrt{3} ;提示: A=2, b=1, \omega=2 , 将 \left(-\frac{\pi}{4}, 0\right) \\ 代入得 \sin \left(-\frac{\pi}{2}+\varphi\right)=-\frac{1}{2}, \because \omega>0,\left(-\frac{\pi}{4}, 0\right)
在单增\\区间上, -\frac{\pi}{2}+\varphi=-\frac{\pi}{6}+2 k \pi, k \in \mathbf{Z}, \because|\varphi|<\frac{\pi}{2}, ~~~~~~~~\\\therefore \varphi=\frac{\pi}{3}, \therefore f(x)=2 \sin \left(2 x+\frac{\pi}{3}\right)
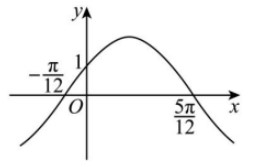
+1, ~~~~~~~~~~~~~~~~~~~~~~~~\\\therefore f\left(\frac{\pi}{2}\right)=1-\sqrt{3} .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 5.\text { 函数 } f(x)=A \sin (\omega x+\varphi)(\omega>0,|\varphi|<\pi) \text { 的部分图像如图所示, }~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案:f(x)=2 \sin \left(2 x+\frac{\pi}{6}\right) ;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\提示:\frac{T}{2}=\frac{5 \pi}{12}-\left(-\frac{\pi}{12}\right) \Rightarrow T=\pi ,\Rightarrow \omega=2 ,将点\\ \left(-\frac{\pi}{12}, 0\right) 带入,得 A \sin \left(-\frac{\pi}{6}+\varphi\right)=0 ,在单增区间,\\\Rightarrow -\frac{\pi}{6}+\varphi=2 k \pi , k \in Z ,又 |\varphi|<\pi ,则 \varphi=\frac{\pi}{6} ,~~\\将点 (0,1) 代入,得 A=2 ,\Rightarrow f(x)=2 \sin \left(2 x+\frac{\pi}{6}\right) . 6.\text { 函数 } f(x)=A \sin (\omega x+\varphi)\left(A>0, \omega>0,|\varphi|<\frac{\pi}{2}\right) 的部分图象如图所示,求函数~~~\\解析式.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
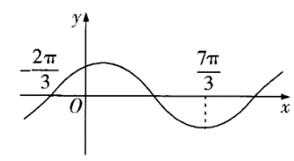
答案f(x)=2\sin(\frac{8}{3}x-\frac{\pi}{6});提示:A=2.根据下面两~~\\图的缩放比例求\omega,左图两红线的距离为\frac{4\pi}{3},右函数距\\离\frac{\pi}{2},由左图变到右图所乘系数为\frac{3}{8},所以\omega所乘系数为\\\frac{8}{3},即为f(x)=2\sin(\frac{8}{3}x+\varphi),代入(\pi,2)得\varphi=-\frac{\pi}{6}. 7.已知函数 f(x)=A \sin (\omega x+\varphi) \mid(A>0, \omega>0,0<\varphi<\pi) 的部分图象如图所示, 且~~ \\ f\left(\frac{13 \pi}{3}\right)=2 .将 f(x) 图象上所有点的横坐标变为原来的 \frac{1}{4} , 再向上平移 1 个单位长度, 得\\到 g(x) 的图象. 若 g\left(x_{1}\right) g\left(x_{2}\right)=9, x_{1}, x_{2} \in[0,4 \pi] , 则 x_{2}-x_{1} 的最大值为 (\quad)~~~~~~~~~~~~~~~~~~~~\\
A. \pi \quad
B. 2 \pi \quad
C. 3 \pi \quad
D. 4 \pi ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案:C;提示:T=4\pi,x=\frac{13 \pi}{3}在\frac{7 \pi}{3}后半个周期,~\\\therefore A=2,\varphi=\frac{\pi}{6},f(x)=2\sin (\frac{x}{2}+\frac{\pi}{6}),\Rightarrow~~~~~~~~~~~~~~~~~~~~~\\g(x)=2\sin (2x+\frac{\pi}{6})+1,又2x+\frac{\pi}{6}\in[\frac{\pi}{6},\frac{13\pi}{6}],画图\\知 2x_{2}-2x_{1}最大值为6\pi,\therefore x_{2}-x_{1} 的最大值为\pi.~~~~~~~~~ 8.已知函数 f(x)=\cos \omega x-1(\omega>0) 在区间 [0,2 \pi] 有且仅有 3 个零点,求 \omega 的取值范围.~~~ 答案
答案: 2 \leqslant \omega<3;提示:\cos \omega x=1, \omega>0, t=\omega x \in[0,2 \omega \pi], \therefore 4 \pi \leqslant 2 \omega \pi<6 \pi, ~~~~~~~~~~~~\\\therefore 2 \leqslant \omega<3~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
9.设函数 f(x)=\sin \left(\omega x+\frac{\pi}{3}\right)(\omega>0) 在区间 (0, \pi) 上恰有三个极值点、两个零点, 求 \omega \\的取值范围.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案: \left(\frac{13}{6}, \frac{8}{3}\right] ;提示: \omega>0, x \in(0, \pi), 令 t=\omega x+\frac{\pi}{3} \in\left(\frac{\pi}{3}, \pi \omega+\frac{\pi}{3}\right) .由 y=\operatorname{sint} 图象\\知 \frac{5 \pi}{2}<\pi \omega+\frac{\pi}{3} \leqslant 3 \pi, \omega 的取值范围为 \left(\frac{13}{6}, \frac{8}{3}\right] .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 10.已知关于 x 的方程 2 \sin ^{2} x-\sqrt{3} \sin 2 x+m-1=0 在 x \in\left(\frac{\pi}{2}, \pi\right) 上有两个不同的实数\\根,求 m 的取值范围.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案 : (-2,-1) ;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
提示:转化为 m=2 \sin \left(2 x+\frac{\pi}{6}\right),~~~~~~~~~~~~~~~~~~~~~~~\\ x \in\left(\frac{\pi}{2}, \pi\right) . 设 2 x+\frac{\pi}{6}=t , 则 t \in\left(\frac{7}{6} \pi, \frac{13}{6} \pi\right) , ~~~\\\therefore \frac{m}{2}=\sin t, t \in\left(\frac{7}{6} \pi, \frac{13}{6} \pi\right), \frac{m}{2} \in\left(-1,-\frac{1}{2}\right) , \\故 m \in(-2,-1) .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 11.已知函数f(x)=2\sin \omega x在区间[-\frac{\pi }{3},\frac{\pi }{4} ]上的最小值为-2,求\omega 的取值范围.~~~~~~~~~~~~~~~~~ 答案
答案:\omega \le-2或\omega \ge \frac{3}{2} ;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\提示:图象过原点,分\omega < 0,\omega > 0讨论. 12.已知函数 y=\cos 2 x ,若将它的图象向左平移 \frac{\pi}{6} 个单位,再将横坐标变为原来的 \frac{1}{3} 倍\\ (纵坐标不变),则得到的函数解析式是( ~~)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\A. y=\cos \left(6 x+\frac{\pi}{3}\right)~~
B. y=-\cos 6 x ~~
C. y=\cos \left(\frac{2}{3} x+\frac{\pi}{3}\right) ~~
D. y=-\cos \frac{2}{3} x
~~~~~~~~~~~~~~~~ 答案
答案:A.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 13.为了得到函数 f(x)=\sin \left(2 x-\frac{\pi}{4}\right) 的图象,只需将函数 g(x)=\cos 2 x 的图象(~~).~~~~~\\A. 向左平移 \frac{3 \pi}{8} 个单位长度~~~~
B. 向右平移 \frac{3 \pi}{8} 个单位长度~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
C. 向左平移 \frac{\pi}{8} 个单位长度~~~~~~
D. 向右平移 \frac{\pi}{8} 个单位长度~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案:B;提示:统一名称,y=\cos 2x=\sin (\frac{\pi}{2}+2x).~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 14.要得到函数 y=\sin \left(2 x+\frac{\pi}{6}\right) 的图象,可以将函数 y=\cos \left(2 x-\frac{\pi}{6}\right) 的图象(~~)~~~~~~~~\\A. 向右平移 \frac{\pi}{12} 个单位长度~~~~
B. 向左平移 \frac{\pi}{12} 个单位长度~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
C. 向右平移 \frac{\pi}{6} 个单位长度~~~~
D. 向左平移 \frac{\pi}{6} 个单位长度~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案:A;提示:统一名称,y=\cos (2x-\frac{\pi}{6})=\sin (\frac{\pi}{2}+2x-\frac{\pi}{6})=\sin (2x+\frac{\pi}{3}).~~~~~~~~~~~~~~