喊你来讲题!
把知识讲给别人是最高效的学习方法!学习金字塔理论和费曼学习法都证明了这一点。咔咔来讲为你提供一个平台,请你来解答下列问题,并将解题过程录制出来,让你因‘分享知识’而进步,让知识因‘被分享’而更有意义。
题目1
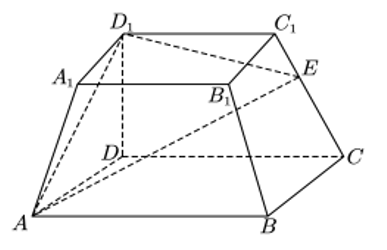
已知四棱台\(ABCD – A_1B_1C_1D_1\)的下底面和上底面分别是边长为4和2的正方形,则( )
A. 侧棱\(CC_1\)上一点\(E\),满足\(\displaystyle \frac{C_1E}{C_1C} = \displaystyle \frac{1}{3}\),则\(A_1B \)//面\(AD_1E\)
B. 若\(E\)为\(CC_1\)的中点,过\(A\),\(D_1\),\(E\)的平面把四棱台分成两部分时,较小部分与较大部分的体积之比为\(3: 5\)
C. \(\overrightarrow{DA} + \overrightarrow{BB_1} + \displaystyle \frac{1}{2}\overrightarrow{DC} = \overrightarrow{DA_1}\)
D. 设\(DB_1\)与面\(AD_1C\)的交点为\(O\),则\(\displaystyle \frac{DO}{OB_1} = \displaystyle \frac{2}{1}\)
答案
答案:$AC$题目2
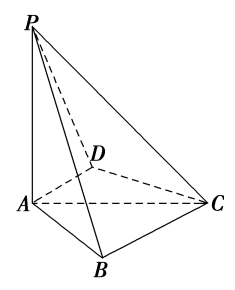
如图,四棱锥\(P-ABCD\)中,\(PA\perp\)底面\(ABCD\),\(PA=AC=2\),\(BC=1\),\(AB=\sqrt{3}\).
(1)若\(AD\perp PB\),证明:\(AD\)//平面\(PBC\);
(2)若\(AD\perp DC\),且二面角\(A-CP-D\)的正弦值为\(\displaystyle \frac{\sqrt{42}}{7}\),求\(AD\).
答案
答案:(1)略;(2)$AD=\sqrt{3}$.题目3
如图,点$P$为正方形$ABCD$所在平面外一点,$M$为$PA$中点,$\overrightarrow{DE}=λ\overrightarrow{DP}(0<λ<1),$平面$ABCD$⊥平面$ABP$,$AB=BP=2,AB⊥BP.$
(1) 当$λ=\displaystyle \frac {2}{3}$时,求证:$PD⊥$平面$BEM$;
(2) 当二面角$D – BM – E$的正弦值为$\displaystyle \frac {\sqrt {6}}{9}$时,求λ的值.
答案
答案:(1)略;(2)$λ=\displaystyle\frac{1}{3}$.题目4
如图,在以$A,B,C,D,E,F$为顶点的五面体中,四边形$ABCD$与四边形$ADEF$均为等腰梯形,$EF// AD,$$BC// AD,$$AD=4,$$AB=$$BC=$$EF=2,$$ED=\sqrt {10},$$FB=2\sqrt {3}$,$M$为$AD$的中点. 求二面角$F – BM – E$的正弦值.
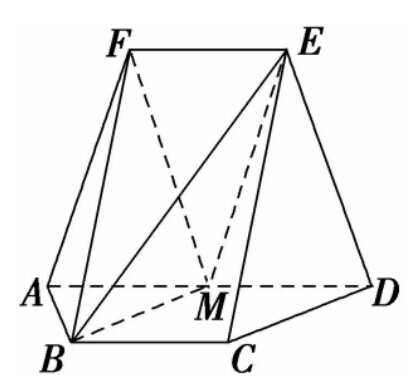
答案
答案:$\displaystyle\frac{4\sqrt{3}}{13}$.题目5
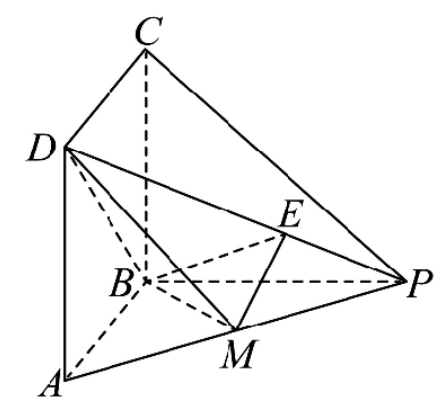
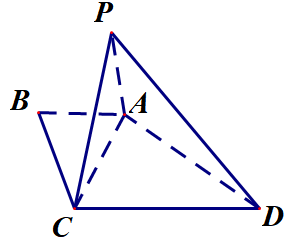
如图,四边形\(ABCD\)中,满足\(AB // CD\),\(\angle ABC = 90^\circ\),\(AB = 1\),\(BC = \sqrt{3}\),\(CD = 2\),将\(\triangle BAC\)沿\(AC\)翻折至\(\triangle PAC\),使得\(PD = 2\).
(1)求证:平面\(PAC \perp\)平面\(ACD\);
(2)求直线\(CD\)与平面\(PAD\)所成角的正弦值.
答案
答案:$\displaystyle\frac{\sqrt{15}}{5}$.题目6
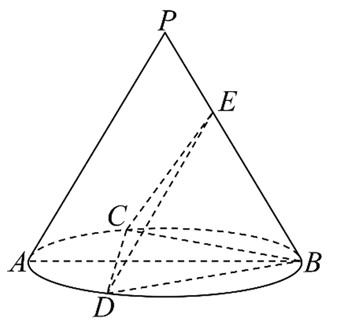
如图,圆锥的轴截面$PAB$是边长为$2$的正三角形,$C$,$D$为底面圆周上的点,且$\triangle BCD$是正三角形,$E$为母线$PB$上的一动点.
(1) 若$PA\parallel$平面$CDE$,求$PE$的长;
(2) 若直线$DE$与平面$BCD$所成角的正弦值为$\dfrac{\sqrt{30}}{10}$,求平面$CDE$与平面$BCD$夹角的余弦值.
答案
答案:(1)$\displaystyle\frac{1}{2}$;(2)$\displaystyle\frac{2\sqrt{7}}{7}$.