观看人数: 673
函数的对称性
1.f(a+x)=f(a-x),f(x)对称轴为:x=a;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
2.f(a+x)=f(b-x),f(x)对称轴为:x=\frac{a+b}{2};~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~3.f(a+x)=-f(a-x),f(x)对称中心为:(a,0);~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
4.f(a+x)+f(a-x)=2b,f(x)对称中心为:(a,b).~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
5. 若函数 y=f(x) 的对称轴为 x=a, x=b , 则其周期为 T=2|b-a| .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
6.若函数 y=f(x) 的对称中心为 (a, 0),(b, 0) , 则其周期为 T=2|b-a| .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
7. 若函数 y=f(x) 的对称轴为 x=a , 对称中心为 (b, 0) , 则其周期为 T=4|b-a| .~~~~~~~~~~~~~~
1.(1)已知定义在 \mathbf{R} 上的函数 f(x) 满足 f(-x)=-f(x), f(1+x)=f(1-x) , 当~~~~~~~~~~~~~~~~\\ x \in [-1,1] 时, f(x)=x^{3}-3 x , 求 f(2023).~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
\\(2)设函数 f(x) 的定义域为 \mathbf{R}, f(x+1) 为奇函数, f(x+2) 为偶函数,当 x \in[0,1] 时, ~~\\ f(x)=2 x^{2}+b x+c ,若 f(3)-f(2)=6 ,则 f\left(\frac{3}{2}\right)=
(\quad)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\A. \frac{9}{4} \quad
B. \frac{3}{2} \quad
C. -\frac{7}{4} \quad
D. -\frac{5}{2} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~答案
答案:(1)2;提示:奇函数,对称轴x=1,周期T=4,f(2023)=f(-1)=2.~~~~~~~~~~~~~~~~
\\(2)D;提示:f(x+1)为奇函数,\Rightarrow (1,0)为对称轴,\therefore f(1)=0;f(x+2)为偶函数,\Rightarrow \\x=2为对称轴,\Rightarrow T=4.★将f(3),f(2),f(\frac{3}{2})全部转化到[0,1].★\Rightarrow b=-8,c=6,\\f(\frac{3}{2})=-f(\frac{1}{2})=-\frac{5}{2}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
2. (1)已知 f(x) 是定义在 \mathbf{R} 上的奇函数, 若 f\left(x+\frac{3}{2}\right) 为偶函数且 f(1) =2 , 求 f(2022)+\\f(2023)+f(2024).~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(2)已知函数f(x)的定义域为\mathrm{R},且f(x + 1) + f(x - 1) = 2,f(x + 2)为偶函数,若~~~~~~~~\\f(0) = 2,则\sum_{k = 1}^{15}f(k) = (\quad)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
A. 116 \quad B. 115\quad C. 114 \quad D. 113~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~答案
答案:(1)4:提示:奇函数,对称轴x=\frac{3}{2},\therefore周期T=6.由对称轴得f(2)=f(1)=2.\\
(2)C;提示:f(-x + 2) = f(x + 2),\Rightarrow x = 2为对称轴.
将x - 1代入得:~~~~~~~~~~~~~~~~~~~~~~\\f(3 - x) = f(x + 1),由已知:f(3 - x) + f(x - 1) = 2,
\Rightarrow (1,1)为对称中心,~~~~~~~~~~~~~~~\\\therefore f(0) = 2,f(1) = 1,f(2) = 0,f(3) = 1,f(4) = 2
\therefore \sum_{k = 1}^{15}f(k) = 114.~~~~~~~~~~~~~~~~~~~~~~~~~~~
3.已知 f(x) 是定义域为 (-\infty,+\infty) 的奇函数, 满足 f(1-x)=f(1+ x) . 若 f(1)=2 , ~~~~~~~~~~\\求 f(1)+f(2)+f(3)+\cdots+f(50).~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案:2;提示:周期T=4,f(1)+f(2)+f(3)+f(4)=2+0-2+0=0.~~~~~~~~~~~~~~~~~
4.
设函数 f(x)=\frac{(x+1)^{2}+\sin x}{x^{2}+1} 的最大值为 M , 最小值为 m , 求 M+m.~~~~~~~~~~~~~~~~~~~~~~~~~~~答案
答案: 2;提示:函数可化简为f(x)=1+\frac{2x+\sin x}{x^{2}+1} ,其中y=\frac{2x+\sin x}{x^{2}+1} 为奇函数,~~~~\\最大值与最小值的和为0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
变式.已知函数f(x)=ax^3+b\sin x+4,f(\lg(\log _210))=5,求f(\lg(\lg2)).~~~~~~~~~~~~~~~~~~~~~~
答案
答案:3;提示:f(\lg(\log_2 10))=f(\lg(\frac{1}{\lg2}))=f(-\lg(\lg 2)),若已知f(t)=5,则~~~~~~~~~~~~~\\f(-t)=3,\therefore f(\lg(\lg2))=3.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
5.已知函数 f(x)(x \in \mathbf{R}) 满足 f(-x)=2-f(x) , 若函数 y=\frac{x+1}{x} 与 y =f(x) 图象的~~~~~~\\交点为 \left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{m}, y_{m}\right) , 求 \sum_{i=1}^{m}\left(x_{i}+y_{j}\right) 的值.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案:m;提示:两个函数的对称中心都是(0,1).~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
6.已知定义在 \mathbf{R} 上的奇函数 f(x) 满足 f(x+2)=-f(x) , 当 1 \leqslant x<2 时, f(x)=x-2 . ~~~\\若 y=\frac{1}{6} x-\frac{1}{3} 与 f(x) 的图象交于点 \left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{n}, y_{n}\right)\left(n \in \mathbf{N}^{*}\right) ,求~~~~~~~~~~~~~~\\ \sum_{i=1}^{n}\left(x_{i}+y_{i}\right).~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~答案
答案:14;提示:两个函数的对称中心都是(2,0).~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
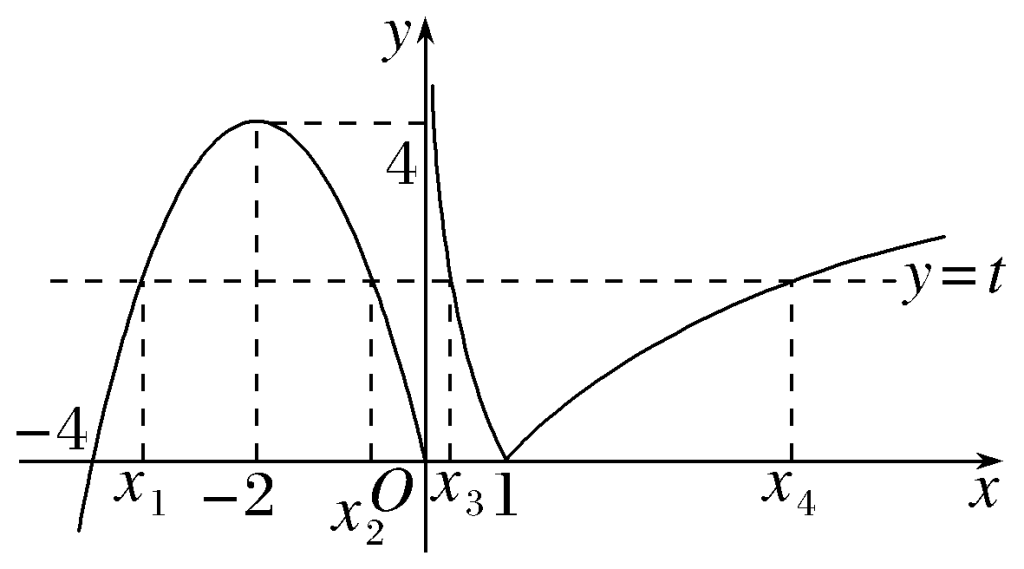
7.已知函数 f(x)=\left\{\begin{array}{l}-x^{2}-4 x, x \leqslant 0, \\ |\log _{2} x \mid, x>0,\end{array}\right. 若 x_{1} < x_{2} < x_{3} < x_{4} ,且 f\left(x_{1}\right)=f\left(x_{2}\right)=~~~~~~~~
\\f\left(x_{3}\right)=f\left(x_{4}\right) ,则下列结论正确的是(\quad)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
A. x_{1}+x_{2}=-4 \quad
B. x_{3} x_{4}=1 \quad
C. 1 < x_{4}<4 \quad
D. 0 < x_{1} x_{2} x_{3} x_{4} \leqslant 4 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案:D;提示:
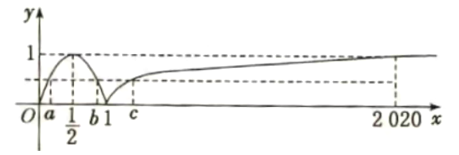
由图象可知 -4 < x_{1} < -2 ,所以 ~~~~~~~\\ x_{1} x_{2} x_{3} x_{4}=x_{1}\left(-4-x_{1}\right)=-x_{1}^{2}-4 x_{1}=\in(0,4) .~~~~~~~ 8.已知函数 f(x)=\left\{\begin{array}{l}\sin \pi x, 0 \leqslant x \leqslant 1, \\ \log _{2020} x, x>1,\end{array}\right. ~
若实数 a, b, c 互不相等,且 f(a)=f(b)=f(c) ,\\则 a+ b+c 的取值范围是 (\quad)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
答案
答案:2 < a+b+c < 2021.~~~~~~~~~~~~~~~~~~~~~~\\提示:图象如图所示,不妨令 a < b < c,~~~\\
由正弦曲线的对称性可知 a+b=1 ,而 ~~~~ \\1 < c < 2020 ,
所以 2 < a+b+c < 2021.
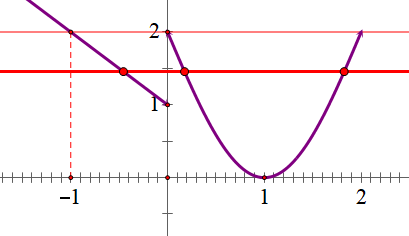
9. 已知函数 f(x)=\left\{\begin{array}{l}2-2 \sin \displaystyle \frac{\pi x}{2}, 0 \leq x \leq 2 \\ -x+1, x<0\end{array}\right. ,若存在实数 x_{1}, ~ x_{2}, ~ x_{3} 且 x_{1} < x_{2} < x_{3} ,~~\\使得 f\left(x_{1}\right)=f\left(x_{2}\right)=f\left(x_{3}\right) ,则 x_{1} f\left(x_{1}\right)+x_{2} f\left(x_{2}\right)+x_{3} f\left(x_{3}\right) 的取值范围为(\quad)~~~~~~~~~~\\
A. \left(-\infty, \frac{9}{2}\right]
B. (-\infty, 2]
C. \left[\frac{9}{4}, \frac{9}{2}\right]
D. \left[2, \frac{9}{4}\right] ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~答案
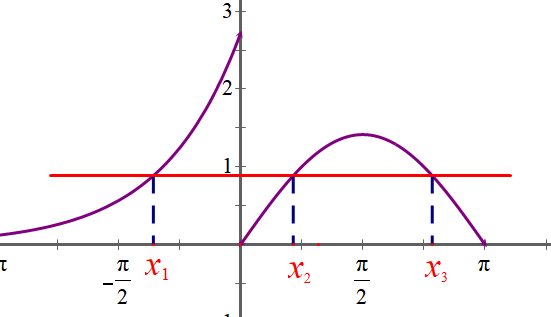
答案:D;提示:x_1\in[-1,0),x_2+x_3=2,~~~~~~~~~~~~~~~~~~~\\ x_{1} f\left(x_{1}\right)+x_{2} f\left(x_{2}\right)+x_{3} f\left(x_{3}\right) =( x_{1}+x_2+x_3) f(x_1)\\(x_1+2)(-x_1+1)\in \left[2, \frac{9}{4}\right] ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 10.已知函数 f(x)=\left\{\begin{array}{l}\mathrm{e}^{x+1}, x \leq 0, \\ \sqrt{2} \sin x, 0 < x \leq \pi\end{array}\right. ,若 y=f(x)-a(a \in \mathbf{R}) 有三个交点 x_{1}, ~~~~\\x_{2}, x_{3} ,若 x_{1} < x_{2} < x_{3} ,求 x_{1}+2 x_{2}+3 x_{3} 的最大值为 .~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~答案
答案:\frac{11\pi}{4}-1;提示:提示:x_{1}+x_{3}=\pi,~~~~~~~~~~~~~~~~\\\therefore x_{1}+2x_{2}+3x_{3}=x_{1}+2(x_{2}+x_{3})+x_{3}~~~~~~~~~~~~~~~~~\\=x_{1}+x_{3}+2\pi,
由图:e^{x_{1}+1}=\sqrt{2}\sin x_{3},~~~~~~~~~~~~\\\therefore x_{1}=\ln\sqrt{2}-1+\ln\sin x_{3}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
\\
\therefore x_{1}+x_{3}+2\pi=\ln\sqrt{2}-1 + 2\pi+x_{3}+\ln\sin x_{3},~\\x_{3}\in(\frac{\pi}{2},\pi),
令g(x)=x+\ln\sin x,~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\g^{\prime}(x)=1+\frac{\cos x}{\sin x}=\frac{\sin x+\cos x}{\sin x},x\in(\frac{\pi}{2},\pi),~~~~~~~~\\
x = \frac{3\pi}{4}为g(x)极大值点,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\\therefore g(\frac{3\pi}{4})=\frac{3\pi}{4}+\ln\frac{\sqrt{2}}{2},\therefore x_{1}+x_{3}+2\pi最大\frac{11\pi}{4}-1.
导函数与原函数的对称性
(1)f(x)为奇函数,则f^{\prime}(x)为偶函数;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\(2)f(x)对称中心为(a,b),则f^{\prime}(x)对称轴为x=a;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
(3)f(x)为偶函数,则f^{\prime}(x)为奇函数;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\(4)f(x)对称轴为x=a,f^{\prime}(x)对称中心为(a,0);~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\(5)f(x)周期为T,f^{\prime}(x)的周期为T.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
1.(多选)已知函数 f(x)(x \in \mathbf{R}) 是奇函数, f(x+2)=f(-x) 且 f(1)=2, f^{\prime}(x) 是 f(x) 的~~~\\导函数,则 (\quad) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
\\A. f(2025)=2 ~~
B. f^{\prime}(x) 的周期是 4~~
C. f^{\prime}(x) 是偶函数~~
D. f^{\prime}(1)=1 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~答案
答案:ABC;提示:f(x+2)=f(-x)\Rightarrow f(x)对称轴为x=1,\Rightarrow f^{\prime}(x) 对称中心~~~~~~~~~~~\\为(1,0),又f(x)为奇,\Rightarrow f(x)周期T=4,f^{\prime}(x) 周期也是4.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
2.已知函数 f(x) 及其导函数 f^{\prime}(x) 的定义域均为 \mathbf{R} , 记 g(x)=f^{\prime}(x) ,若 f(x+2) 为偶函数,\\ g(x) 为奇函数,则 (\quad)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\
A. f(x)=f(4-x) ~~
B. g(x)=-g(4-x) ~~
C. f(x)=-f(x+4) ~~
D. g(x)=g(x+4) ~~~~~~~~~答案
答案:ABD;提示:f(x+2)为偶,g(x)对称中心为(2,0),又g(x)为奇,\therefore g(x)周期~~~~\\T=4,\therefore BD正确.f(x+2) 为偶函数,\therefore f(x)对称轴为x=2,A正确.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
3.已知函数 f(x) 是定义在 \mathbf{R} 上的可导函数, 其导函数为 g(x), f(x+2) 和 g(x+1) 都是奇\\函数, f(1)=1 , 则下列说法正确的是 (~~ )~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
A. g(x) 关于点 (1,0) 对称~~
B. f(x)+f(-x)=0 ~~
C. g(2025)=1 ~~
D. \sum_{k=0}^{2024} f(k)=0 ~~~~~~~~~~~~~~~答案
答案:ABD;提示: g(x)=f^{\prime}(x),f(x+2)为奇函数,\Rightarrow f(x)对称中心为(2,0)且g(x)\\对称轴为x=2;g(x+1)为奇函数,\Rightarrow g(x)对称中心为(1,0)且f(x)对称轴为x=1.~~~~~
4.已知函数 f(x) 及其导函数 f^{\prime}(x) 定义域均为 R ,满足 f\left(\frac{3}{2}+x\right)-f\left(\frac{3}{2}-x\right)=2 x ,记~\\ g(x)=f^{\prime}(x) ,其导函数为 g^{\prime}(x) ,且 g^{\prime}(3-x) 的图象关于原点对称,求 g^{\prime}(9)+g\left(\frac{9}{2}\right)的值.
答案
答案:1;提示:
因为f(\frac{3}{2}+x)-f(\frac{3}{2}-x)=2x,求导得f'(\frac{3}{2}+x)+f'(\frac{3}{2}-x)=2.~~~~~~~~\\
即g(\frac{3}{2}+x)+g(\frac{3}{2}-x)=2 ①,再求导得g'(\frac{3}{2}+x)-g'(\frac{3}{2}-x)=0 ② .
g'(3 + x)=~~~~~~~~~~\\ - g'(3 - x) ③ .
由②、③可知g'(x)对称轴为x =\frac{3}{2},对称中心为(3,0) ,则周期T = 6.~~~~~~~~~~~\\
因为g'(9) = g'(3) = 0.
由③得原函数g(x)对称轴为x = 3,由①⇒g(x)对称中心为(\frac{3}{2},1) .\\
因为g(\frac{9}{2}) = g(6 - \frac{1}{2}) = g(\frac{3}{2}) = 1,所以g'(\frac{9}{2}) + g(\frac{3}{2}) = 1.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~